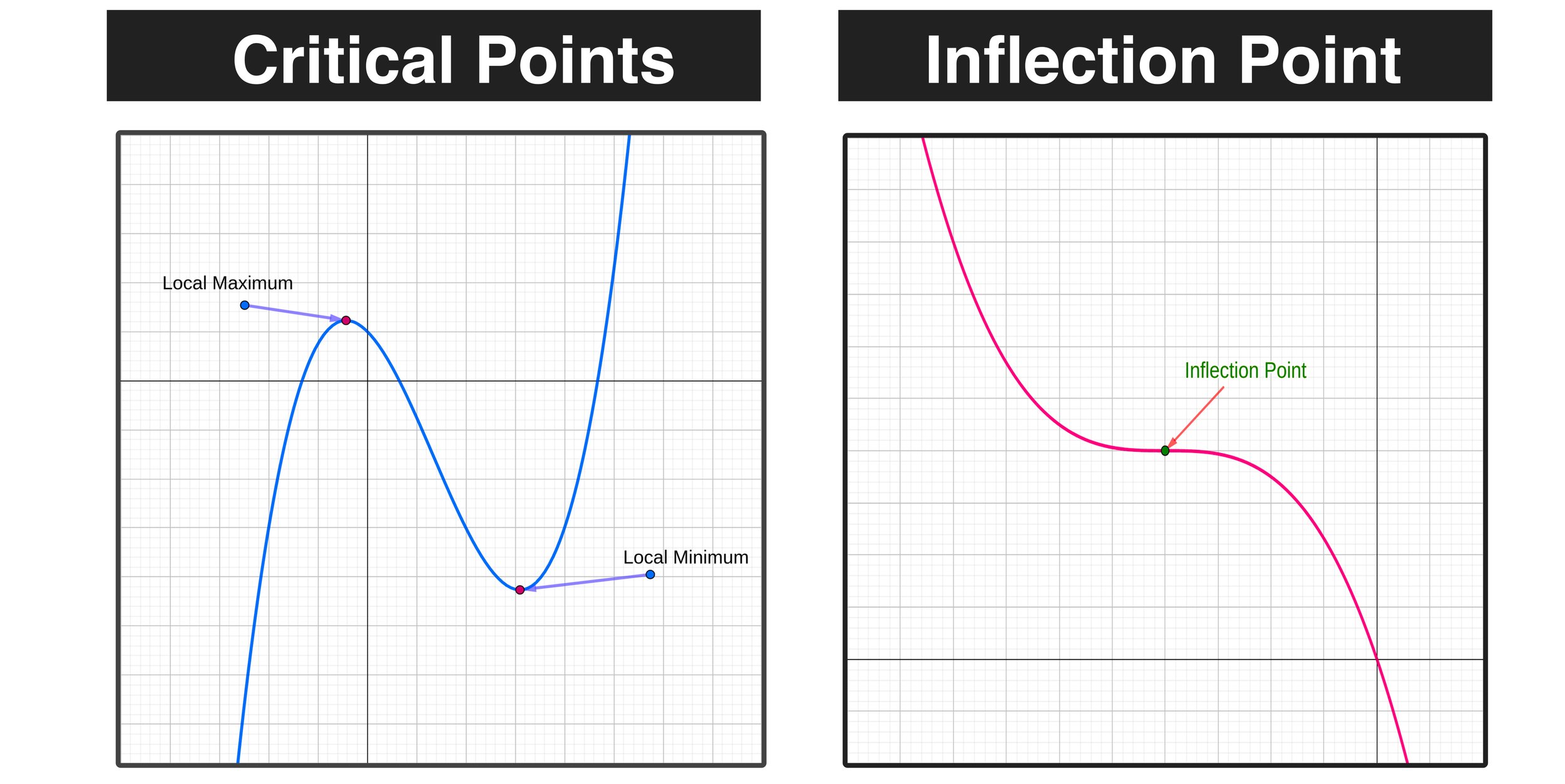
Point Of Inflection And Maximum . The inflection points of a function are stationary points where the slope is equal to zero. That is, at an inflection point we have $latex \frac{dy}{dx}=0$. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Inflection points are points where the function changes concavity, i.e. They may occur if f(x) = 0 or if f(x) is. In this article, the concept and meaning of. When the second derivative is negative, the function is concave downward. You can think of potential inflection points as critical points for the first derivative — i.e. And the inflection point is where it goes from concave upward to concave downward (or vice versa). A global maximum is a point that takes the largest value on the entire range of the function, while a global minimum is the point.
from www.mashupmath.com
That is, at an inflection point we have $latex \frac{dy}{dx}=0$. And the inflection point is where it goes from concave upward to concave downward (or vice versa). You can think of potential inflection points as critical points for the first derivative — i.e. The inflection points of a function are stationary points where the slope is equal to zero. Inflection points are points where the function changes concavity, i.e. They may occur if f(x) = 0 or if f(x) is. In this article, the concept and meaning of. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. A global maximum is a point that takes the largest value on the entire range of the function, while a global minimum is the point. When the second derivative is negative, the function is concave downward.
How to Graph a Function in 3 Easy Steps — Mashup Math
Point Of Inflection And Maximum They may occur if f(x) = 0 or if f(x) is. And the inflection point is where it goes from concave upward to concave downward (or vice versa). When the second derivative is negative, the function is concave downward. The inflection points of a function are stationary points where the slope is equal to zero. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. They may occur if f(x) = 0 or if f(x) is. You can think of potential inflection points as critical points for the first derivative — i.e. In this article, the concept and meaning of. A global maximum is a point that takes the largest value on the entire range of the function, while a global minimum is the point. That is, at an inflection point we have $latex \frac{dy}{dx}=0$. Inflection points are points where the function changes concavity, i.e.
From www.linstitute.net
AQA A Level Maths Pure复习笔记7.2.4 Stationary Points & Turning Points翰林国际教育 Point Of Inflection And Maximum In this article, the concept and meaning of. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. When the second derivative is negative, the function is concave downward. The inflection points of a function are stationary points where the slope is equal to zero. A global maximum is a. Point Of Inflection And Maximum.
From www.pinterest.com
Inflection Points the points at which a product a trend Point Of Inflection And Maximum They may occur if f(x) = 0 or if f(x) is. A global maximum is a point that takes the largest value on the entire range of the function, while a global minimum is the point. And the inflection point is where it goes from concave upward to concave downward (or vice versa). In this article, the concept and meaning. Point Of Inflection And Maximum.
From www.youtube.com
Inflection points (algebraic) AP Calculus AB Khan Academy YouTube Point Of Inflection And Maximum In this article, the concept and meaning of. And the inflection point is where it goes from concave upward to concave downward (or vice versa). They may occur if f(x) = 0 or if f(x) is. You can think of potential inflection points as critical points for the first derivative — i.e. Inflection points are points where the function changes. Point Of Inflection And Maximum.
From en.neurochispas.com
Maxima, Minima and Inflection Points of Functions Neurochispas Point Of Inflection And Maximum A global maximum is a point that takes the largest value on the entire range of the function, while a global minimum is the point. That is, at an inflection point we have $latex \frac{dy}{dx}=0$. The inflection points of a function are stationary points where the slope is equal to zero. Inflection points are points where the function changes concavity,. Point Of Inflection And Maximum.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection And Maximum The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Inflection points are points where the function changes concavity, i.e. They may occur if f(x) = 0 or if f(x) is. The inflection points of a function are stationary points where the slope is equal to zero. That is, at. Point Of Inflection And Maximum.
From calcworkshop.com
The Second Derivative Test (HowTo w/ 15 StepbyStep Examples!) Point Of Inflection And Maximum In this article, the concept and meaning of. You can think of potential inflection points as critical points for the first derivative — i.e. And the inflection point is where it goes from concave upward to concave downward (or vice versa). When the second derivative is negative, the function is concave downward. The inflection points of a function are stationary. Point Of Inflection And Maximum.
From www.nagwa.com
Question Video Finding the Inflection Points of a Function from the Point Of Inflection And Maximum Inflection points are points where the function changes concavity, i.e. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. The inflection points of a function are stationary points where the slope is equal to zero. A global maximum is a point that takes the largest value on the entire. Point Of Inflection And Maximum.
From www.slideserve.com
PPT C2 Chapter 9 Differentiation PowerPoint Presentation, free Point Of Inflection And Maximum Inflection points are points where the function changes concavity, i.e. That is, at an inflection point we have $latex \frac{dy}{dx}=0$. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. You can think of potential inflection points as critical points for the first derivative — i.e. And the inflection point. Point Of Inflection And Maximum.
From www.youtube.com
Inflection Points YouTube Point Of Inflection And Maximum The inflection points of a function are stationary points where the slope is equal to zero. And the inflection point is where it goes from concave upward to concave downward (or vice versa). That is, at an inflection point we have $latex \frac{dy}{dx}=0$. In this article, the concept and meaning of. A global maximum is a point that takes the. Point Of Inflection And Maximum.
From www.cuemath.com
Applications of Derivatives Definition, Applications, Properties Point Of Inflection And Maximum You can think of potential inflection points as critical points for the first derivative — i.e. When the second derivative is negative, the function is concave downward. Inflection points are points where the function changes concavity, i.e. In this article, the concept and meaning of. The point where the function is neither concave nor convex is known as inflection point. Point Of Inflection And Maximum.
From www.storyofmathematics.com
Absolute maximum Definition, Conditions, and Examples Point Of Inflection And Maximum And the inflection point is where it goes from concave upward to concave downward (or vice versa). When the second derivative is negative, the function is concave downward. In this article, the concept and meaning of. A global maximum is a point that takes the largest value on the entire range of the function, while a global minimum is the. Point Of Inflection And Maximum.
From www.youtube.com
Optimisation in Economics Maximum and Minimum Value of a Function Point Of Inflection And Maximum You can think of potential inflection points as critical points for the first derivative — i.e. The inflection points of a function are stationary points where the slope is equal to zero. When the second derivative is negative, the function is concave downward. In this article, the concept and meaning of. They may occur if f(x) = 0 or if. Point Of Inflection And Maximum.
From www.youtube.com
Inflexion Point YouTube Point Of Inflection And Maximum You can think of potential inflection points as critical points for the first derivative — i.e. That is, at an inflection point we have $latex \frac{dy}{dx}=0$. They may occur if f(x) = 0 or if f(x) is. In this article, the concept and meaning of. A global maximum is a point that takes the largest value on the entire range. Point Of Inflection And Maximum.
From aliarnn.blogfa.com
نحوه یافتن و طبقه بندی نقاط ثابت Point Of Inflection And Maximum You can think of potential inflection points as critical points for the first derivative — i.e. And the inflection point is where it goes from concave upward to concave downward (or vice versa). When the second derivative is negative, the function is concave downward. In this article, the concept and meaning of. That is, at an inflection point we have. Point Of Inflection And Maximum.
From www.youtube.com
Given a graph of f' learn to find the points of inflection YouTube Point Of Inflection And Maximum Inflection points are points where the function changes concavity, i.e. The inflection points of a function are stationary points where the slope is equal to zero. And the inflection point is where it goes from concave upward to concave downward (or vice versa). The point where the function is neither concave nor convex is known as inflection point or the. Point Of Inflection And Maximum.
From www.slideserve.com
PPT How to find the absolute minimum and maximum values PowerPoint Point Of Inflection And Maximum Inflection points are points where the function changes concavity, i.e. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. A global maximum is a point that takes the largest value on the entire range of the function, while a global minimum is the point. That is, at an inflection. Point Of Inflection And Maximum.
From www.youtube.com
Point of inflection and point of inflexion YouTube Point Of Inflection And Maximum When the second derivative is negative, the function is concave downward. Inflection points are points where the function changes concavity, i.e. In this article, the concept and meaning of. They may occur if f(x) = 0 or if f(x) is. You can think of potential inflection points as critical points for the first derivative — i.e. The inflection points of. Point Of Inflection And Maximum.
From www.youtube.com
Part I Find the Local Max/Min Point, Inflection Points and Determine Point Of Inflection And Maximum And the inflection point is where it goes from concave upward to concave downward (or vice versa). Inflection points are points where the function changes concavity, i.e. A global maximum is a point that takes the largest value on the entire range of the function, while a global minimum is the point. You can think of potential inflection points as. Point Of Inflection And Maximum.